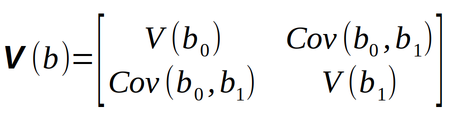O estudo "empírico" de um Sistema Físico, Químico ou Biológico (ou suas combinações) consiste essencialmente em identificar quais os fatores que podem influenciar o comportamento (respostas) do(s) sistema(s).
Em um primeiro momento, o objetivo é planejar experimentos que permitam identificar quais são os fatores importantes, para em seguida realizar experimentos complementares que permitam desenvolver um “modelo” (estatístico ou mecanístico) que “descreva”, de forma qualitativa ou quantitativa, a relação entre os “fatores causais” e a(s) respectiva(s) resposta(s) como mostra a figura Y.1.
Figura Y.1. Um sistema pode ser representado por uma função (em princípio desconhecida) ligando os fatores (variáveis de entrada) às respostas (variáveis de saída). (Fonte: Como fazer experimentos, 2001)
Talvez o principal desafio no uso das técnicas de “Planejamento de Experimentos” seja “reprogramar a nossa mente” para exercitar um “Pensamento Multifatorial ou Multivariado”, já que muitos de nós, pelo menos da minha geração, não tiveram acesso a esses conhecimentos.
E muitos dos que tiveram contato com os conceitos teóricos, provavelmente tiveram dificuldades para aplicar essas técnicas no seu cotidiano profissional (em universidades ou empresas) devido às dificuldades para o acesso a programas (sofwares) estatísticos “amigáveis e acessíveis”.
Alguns programas oferecem “muitas” funcionalidades. Mas o excesso de funcionalidades acaba gerando uma certa complexidade no seu uso devido ao grande número de telas e menus para a seleção das diferentes opções de configuração.
Outra questão é o custo das licenças.
Não é viável o uso de programas proprietários, sem o pagamento de licenças, dentro das organizações (empresas ou universidades), e isso se torna um outro obstáculo já que o preço das licenças de alguns programas estatísticos não é acessível a muitas organizações.
Já existem muitos textos teóricos na Internet explicando os fundamentos estatísticos das técnicas de “Planejamento de Experimentos” (DOE - Design Of Experiments). Por isso vamos direto à aplicação prática da técnica de “Planejamento Fatorial Completo em Dois Níveis”, usando a linguagem Python para a realização dos cálculos.
A primeira etapa é montar uma “matriz de planejamento” com todas as possíveis combinações dos “n” fatores em “2” níveis.
Por exemplo, para estudar o efeito da Temperatura (T) e do tipo de Catalisador (C) no rendimento (%) de uma reação precisamos definir os “níveis” de cada fator.
Considere o nível alto da temperatura em 60 °C e o nível baixo em 40 °C. E os dois níveis do catalisador como dois dipos: catalisador A e catalisador B.
Neste caso a temperatura é uma variável “quantitativa” e o catalisador é uma variável “qualitativa” (ou categórica).
Com 2 fatores em 2 níveis diferentes teremos 4 (22) possíveis combinações e consequentemente 4 diferentes condições experimentos indicados na tabela Y.1, chamada de “Matriz de Planejamento”.
Tabela Y.1. Matriz de planejamento para o estudo da variação do rendimento da reação em função da temperatura, na faixa de 30-70°C, e do tipo de catalisador (A ou B). (Fonte: Como fazer experimentos, 2001)
| Experimento (ou Ensaio) | Temperatura (°C) | Catalisador | Rendimento (%) |
|---|---|---|---|
| 1 | 40 | A | |
| 2 | 40 | B | |
| 3 | 60 | A | |
| 4 | 60 | B |
Em seguida a Matriz de Planejamento da tabela Y.1 é reescrita substituindo os níveis superiores dos fatores por “+1” e os níveis inferiores por “-1” como mostra a tabela Y.2, chamada de “Matriz de Planejamento com Variáveis Codificadas”.
Vamos considerar “arbitrariamente” o catalisador A como -1 e B como +1.
Tabela Y.2. Matriz de planejamento com variáveis codificadas para o estudo da variação do rendimento da reação em função da temperatura, na faixa de 30-70°C, e do tipo de catalisador (A ou B). (Fonte: Como fazer experimentos, 2001)
| Experimento (ou Ensaio) | Temperatura (°C) | Catalisador | Rendimento (%) |
|---|---|---|---|
| 1 | -1 | -1 | |
| 2 | -1 | 1 | |
| 3 | 1 | -1 | |
| 4 | 1 | 1 |
A “Tabela de Planejamento com Variáveis Codificadas” é convertida na “Tabela de Coeficientes de Contraste” acrescentando uma coluna de “uns” à esquerda para o cálculo da média das respostas.
E à direita é acrescentada a coluna correspondente à interação entre Temperatura e Catalisador (interação TC) que corresponde aos produtos, elemento a elemento, dos códigos das colunas T e C.
Dessa forma obtemos uma tabela 4 x 4 como mostra a tabela Y.3.
Tabela Y.3. Matriz de planejamento com variáveis codificadas para o estudo da variação do rendimento da reação em função da temperatura, na faixa de 30-70°C, e do tipo de catalisador (A ou B). (Fonte: Como fazer experimentos, 2001)
| Média | Temperatura | Catalisador | Temperatura × Catalisador |
|---|---|---|---|
| 1 | -1 | -1 | 1 |
| 1 | -1 | 1 | -1 |
| 1 | 1 | -1 | -1 |
| 1 | 1 | 1 | 1 |
Com a Tabela de Coeficientes de Contraste vamos calcular o modelo estatístico que descreve as respostas de um planejamento fatorial em termos dos efeitos por unidade de variação dos fatores.
Vamos importar as bibliotecas NumPy, Pandas e itertools:
>>> import numpy as np >>> import pandas as pd >>> import itertools
Solicitar o número de fatores (Ex: n=2) e armazenar na variável n_factors:
>>> n_factors = int(input("Por favor, digite o número de fatores: "))
Por favor, digite o número de fatores: 2
>>>
Gerar todas as combinações dos fatores nos níveis alto e baixo e armazenar na variável exp_plan_coded_var, que corresponde à “matriz de planejamento com variáveis codificadas”:
>>> exp_plan_coded_var = np.array(list(itertools.product([-1,1], repeat = n_factors)))
>>> exp_plan_coded_var
array([[-1, -1],
[-1, 1],
[ 1, -1],
[ 1, 1]])
A primeira coluna representa o fator Temperatura e os números +1 e -1 correspondem aos níveis alto (60) e baixo (40) respectivamente.
A segunda coluna represanta o fator Catalisdor e os números +1 e -1 correspondem aos níveis alto (A) e baixo (B) respectivamente.
Em seguida vamos criar a variável dict_factors que irá armazenar informações importantes sobre o planejamento experimental:
#Dictionary with info about the Experimental Planning
dict_factors = {}
E implementar um loop for que solicita o nome de cada fator, com os respectivos limites superior (+1) e inferior (-1), e cria um identificador para cada fator (x1, x2, ... xn), que será a chave principal do dicionário dict_factors:
>>> #Dictionary with info about the Experimental Planning
... dict_factors = {}
>>>
>>> for i in range(n_factors):
... code_factor = 'x' + str(i+1)
... #dict_factors[code_factor] = {'id_column' : i}
... name = input("Por favor, digite o nome do fator %d :" % (i+1))
... name_factor = name
... level_inf = input("Por favor, digite o nível INFERIOR do fator %d :" % (i+1))
... level_sup = input("Por favor, digite o nível SUPERIOR do fator %d :" % (i+1))
... dict_factors[code_factor] = {'name_factor' : name_factor, 'level_sup' : level_sup, 'level_inf' : level_inf, 'id_column' : i}
...
Por favor, digite o nome do fator 1 :Temperatura
Por favor, digite o nível INFERIOR do fator 1 :40
Por favor, digite o nível SUPERIOR do fator 1 :60
Por favor, digite o nome do fator 2 :Catalisador
Por favor, digite o nível INFERIOR do fator 2 :B
Por favor, digite o nível SUPERIOR do fator 2 :A
E para visualizar as informações armazenadas na variável dict_factors:
>>> print("dict_factors: \n", dict_factors)
dict_factors:
{'x1': {'level_inf': '40', 'level_sup': '60', 'name_factor': 'Temperatura', 'id_column': 0}, 'x2': {'level_inf': 'B', 'level_sup': 'A', 'name_factor': 'Catalisador', 'id_column': 1}}
>>> for k in dict_factors:
... print("Código do fator: %s, Id da coluna: %d" % (k , dict_factors[k]['id_column']))
...
Código do fator: x1, Id da coluna: 0
Código do fator: x2, Id da coluna: 1
O conteúdo da variável exp_plan_coded_var (Matriz de Planejamento com Variáveis Codificadas) é copiado para a variável contrast_coef_table (Tabela de Coeficientes de Contraste), que será usada para o cálculo do modelo estatístico correspondente ao planejamento.
>>> contrast_coef_table = np.copy(exp_plan_coded_var)
>>> contrast_coef_table
array([[-1, -1],
[-1, 1],
[ 1, -1],
[ 1, 1]])
>>>
Um dicionário não é ordenado automaticamente, por isso vamos ordenar as “chaves” (keys) do dicionário dict_factors na variável lista sorted_factors:
>>> sorted_factors = sorted(dict_factors, key=lambda x: (dict_factors[x]['id_column'])) >>> sorted_factors ['x1', 'x2']
Na etapa seguinte utilizamos uma sequência de 3 loops for aninhados para montar a lista com todas as possíveis interações entre os fatores e uma lista com todos os termos do modelo estatístico.
>>> list_all_interactions = [] >>> list_all_terms_of_statistical_model = [] >>>for f in sorted_factors: ... list_all_terms_of_statistical_model.append(f) ... >>> for n in range(2, n_factors+1): ... list_interactions = list(itertools.combinations(sorted_factors, n)) ... list_all_interactions.append(list_interactions) ... for c in range(len(list_interactions)): ... n_factors_in_combination = len(list_interactions[c]) ... list_all_terms_of_statistical_model.append(list_interactions[c]) ... temp_column = np.ones((exp_plan_coded_var.shape[0], 1)) ... for f in range(len(list_interactions[c])): ... dict_factors_key = list_interactions[c][f] ... id_column_of_factor = dict_factors[dict_factors_key]['id_column'] ... selected_column_coded_var = exp_plan_coded_var[:, id_column_of_factor].reshape(-1,1) ... temp_column = np.multiply(temp_column, selected_column_coded_var) ... contrast_coef_table = np.hstack([contrast_coef_table, temp_column]) ... >>>
E para visualizar o conteúdo das variáveis:
>>> print("sorted_factors: \n", sorted_factors)
sorted_factors:
['x1', 'x2']
>>> print("List of all interactions: \n", list_all_interactions)
List of all interactions:
[[('x1', 'x2')]]
>>> print("contrast_coef_table AFTER loop: \n", contrast_coef_table, contrast_coef_table.shape)
contrast_coef_table AFTER loop:
[[-1. -1. 1.]
[-1. 1. -1.]
[ 1. -1. -1.]
[ 1. 1. 1.]] (4, 3)
>>>
Em seguida vamos complementar a “Tabela de Coeficientes de Contraste” adicionando uma coluna de “uns” à esquerda que permitirá calcular a “média das respostas”:
>>> column_ones = np.ones((exp_plan_coded_var.shape[0],1))
>>> contrast_coef_table = np.hstack([column_ones, contrast_coef_table])
>>> print("contrast_coef_table AFTER APPENDING a column of ones: \n", contrast_coef_table, contrast_coef_table.shape)
contrast_coef_table AFTER APPENDING a column of ones:
[[ 1. -1. -1. 1.]
[ 1. -1. 1. -1.]
[ 1. 1. -1. -1.]
[ 1. 1. 1. 1.]] (4, 4)
>>>
Para simplificar a notação vamos copiar a “Tabela de Coeficientes de Contraste” para a variável X:
>>> X = np.copy(contrast_coef_table)
>>> X
array([[ 1., -1., -1., 1.],
[ 1., -1., 1., -1.],
[ 1., 1., -1., -1.],
[ 1., 1., 1., 1.]])
>>>
Os resultados de rendimento obtidos nos experimentos indicados na tabela Y.1 são organizados em um arquivo csv com a seguinte estrutura:
Rendimento 59 54 90 68
Crie esse arquivo em uma planilha e salve no forma “CSV” com o nome que quiser (mas no mesmo diretório onde estiver executando o programa), definindo como delimitador de campo o caracter “;”.
Em seguida use o comando input e digite o nome do arquivo, que foi chamado de Rend_Plan_Exp_Temp_Cat.csv.
>>> Y_csv_file = input("Por favor, digite o nome do arquivo com os resultados dos experimentos: ")
Por favor, digite o nome do arquivo com os resultados dos experimentos: Rend_Plan_Exp_Temp_Cat.csv
>>> print("Y_csv_file:", Y_csv_file)
Y_csv_file: Rend_Plan_Exp_Temp_Cat.csv
O conteúdo do arquivo Rend_Plan_Exp_Temp_Cat.csv é lido com o comando pd.read_csv e armazenado como um dataframe na variável Y_df contendo os rendimentos obtidos em cada experimento na ordem correspondente à tabela Y.1.
>>> Y_df = pd.read_csv(Y_csv_file, sep = ';', decimal=',') >>> Y_df Rendimento 0 59 1 54 2 90 3 68
E a matriz de planejamento com os resultados de rendimento (%) das reações incluídos fica conform a tabela Y.4.
Tabela Y.4. Matriz de planejamento completa para o estudo da variação do rendimento da reação em função da temperatura, na faixa de 30-70°C, e do tipo de catalisador (A ou B). (Fonte: Como fazer experimentos, 2001)
| Experimento (ou Ensaio) | Temperatura (°C) | Catalisador | Rendimento (%) |
|---|---|---|---|
| 1 | 40 | A | 59 |
| 2 | 40 | B | 54 |
| 3 | 60 | A | 90 |
| 4 | 60 | B | 68 |
Agora com todas as informações disponíveis podemos executar as operações matriciais para o cálculo da matriz (B) com os coeficientes do modelo estatístico correspondente ao planejamento.
As variáveis “dependentes” são convertidas do formato “dataframe” para “array” com o comando:
>>> Y = Y_df.values[:]
>>> Y
array([[59],
[54],
[90],
[68]])
>>>
Matriz transposta de X:
>>> X_t = X.T
>>> X_t
array([[ 1., 1., 1., 1.],
[-1., -1., 1., 1.],
[-1., 1., -1., 1.],
[ 1., -1., -1., 1.]])
Produto matricial de X_t por X:
>>> X_t_dot_X = np.dot(X_t, X)
>>> X_t_dot_X
array([[4., 0., 0., 0.],
[0., 4., 0., 0.],
[0., 0., 4., 0.],
[0., 0., 0., 4.]])
Matriz inversa:
>>> inv_X_t_dot_X = np.linalg.inv(X_t_dot_X)
>>> inv_X_t_dot_X
array([[0.25, 0. , 0. , 0. ],
[0. , 0.25, 0. , 0. ],
[0. , 0. , 0.25, 0. ],
[0. , 0. , 0. , 0.25]])
Produto matricial de X_t por Y:
>>> X_t_dot_Y = np.dot(X_t, Y)
>>> X_t_dot_Y
array([[271.],
[ 45.],
[-27.],
[-17.]])
Cálculo da matriz de coeficientes do modelo (B):
>>> B = np.dot(inv_X_t_dot_X, X_t_dot_Y)
>>> B
array([[67.75],
[11.25],
[-6.75],
[-4.25]])
Vamos agora “montar” o modelo estatístico que será armazenado na variável statistical_model iteragindo ao longo das linhas da matriz B e da lista de todas as interações (list_all_interactions).
Armazenando o primeiro elemento da matriz B correspondente à média dos rendimentos:
>>> statistical_model = str(B.item(0)) >>> statistical_model '67.75'
Iterando sobre as linhas da matriz B e a lista de todas as interações para montar o modelo estatístico:
>>> for coef, factor in zip(B[1:], list_all_terms_of_statistical_model):
... if coef.item() > 0:
... statistical_model = statistical_model + ' +'
... statistical_model = statistical_model + str("%.4f" % coef.item()) + ' * '
... statistical_model = statistical_model + str(factor)
... statistical_model = statistical_model + ' '
...
>>> statistical_model
"67.75 +11.2500 * x1 -6.7500 * x2 -4.2500 * ('x1', 'x2') "
Portanto o modelo estatístico que descreve os efeitos individuais da Temperatura (T) e do Catalisador (C) e o efeito da interação (TC) no Rendimento (R) da reação é dado pela equação Y.1:
Equação Y.1. Modelo estatístico resultante do planejamento fatorial 22 que descreve os efeitos individuais da Temperatura (T) e do Catalisador (C) e o efeito da interação (TC) no Rendimento (R) da reação
67,75 + 11,25 × T −6,75 × C −4,25 × TC
Na matriz de planejamento com variáveis codificadas (Tabela Y.2) os valores dos fatores (T e C) foram substituídos por +1 ou -1, o que corresponde a uma “transformação” das variáveis originais.
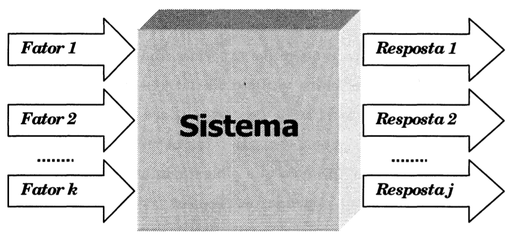
Por exemplo, a transformação dos limites inferior (40°C) e superior (60°) da temperatura em -1 e +1 respectivamente, é feita subtraindo de cada um deles o valor médio (50°C) e dividindo o resultado pela metade do intervalo (diferença entre o limite superior e o inferior) como mostra a figura Y.2
Figura Y.2. Exemplo de aplicação da fórmula de transformação de fatores para a codificação dos limites de Temperatura (Fonte: Como fazer experimentos, 2001)
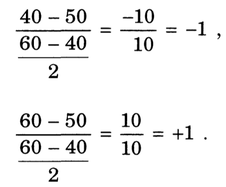
Isto significa, obviamente, colocar a origem do eixo das temperaturas no valor intermediário, 50°C, e definir uma nova escala, em que cada unidade corresponde a 10oe. Da mesma forma, a codificação fará com que a origem do eixo dos catalisadores fique centrada entre os catalisadores A e B, numa espécie de "nível zero" sem qualquer significado físico mas que, do ponto de vista algébrico, pode ser tratado do mesmo modo que a origem das temperaturas. (Fonte: Como fazer experimentos, 2001)
A transformação está ilustrada na figura Y.3, onde as variáveis temperatura e catalisador passam a ser chamadas, depois de codificadas, de x1 e x2 respectivamente.
Figura Y.3. Transformação das variáveis do planejamento 22, na qual a origem do novo sistema de coordenadas está localizada na média de todas as respostas. E a unidade em cada eixo é a metade da amplitude de variação do fator correspondente. (Fonte: Como fazer experimentos, 2001)
A média dos Rendimentos obtidos (67,75%) correspondente à origem do novo sistema de eixos e é indicado pelo primeiro termo do modelo estatísticos (Equação Y.1).
O modelo estatístico usado para descrever as respostas de um planejamento fatorial é formulado em termos dos efeitos por unidade de variação dos fatores. Ou seja, quando um fator passa de -1 para +1 isso significa um aumento de “2 unidades” do fator correspondente.
Por exemplo, quando a temperatura passa de 40 °C (-1) para 60 °C (+1) isso significa um aumento de 2 unidades do fator x1 (+1 - (-1) = 2). E como o coeficiente de x1, segundo o modelo, vale +11.25, isso representa uma contribuição positiva de 22,5% (2 × 11,25) no rendimento da reação.
Entendeu? ;-)
E quanto aos efeitos do Catalisador e da interação Temperatura×Catalisador (TC)?
Vamos considerar “por enquanto” que o efeitos são “estatísticamente significativos”, e usar o gráfico da figura Y.4 para interpretar os efeitos.
Figura Y.4. Diagrama com os rendimentos obtidos nas 4 condições do planejamento fatorial 22. (Fonte: Como fazer experimentos, 2001)
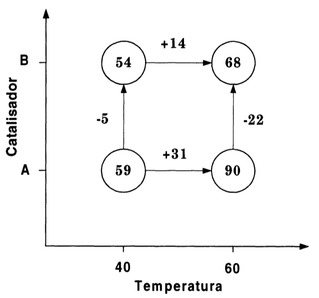
Como o efeito de interação é significativo, os efeitos principais devem ser interpretados conjuntamente obtendo-se as seguintes conclusões: (Fonte: Como fazer experimentos, 2001)
Elevando a temperatura aumentamos o rendimento da reação, mas esse efeito é muito mais pronunciado com o catalisador A do que com o catalisador B (+31% contra +14%).
Trocando o catalisador A pelo catalisador B diminuímos o rendimento da reação, e esse efeito é muito mais significativo a 60°C do que a 40°C ( -22% contra -5%).
Os maiores rendimentos (90%, em média) são obtidos com o catalisador A e com a temperatura em 60°C.
Nota
Mas é importante ressaltar que o modelo obtido é válido para os “pontos experimentais” do planejamento. E portanto, a rigor, não pode ser interpretado como uma equação que possa ser extrapolada ou interpolada, porque os valores das variáveis codificadas, x1 e x2 estão restritos a +1 ou -1.
Agora é necessário avaliar a significância estatística dos efeitos e identificar quais efeitos são “estatísticamente significativos” e quais são apenas variações do “erro experimental”.
Os intervalos de confiança dos parâmetros podem ser calculados pela equação Y.2
Equação Y.2. Equação para o cálculo do intervalo de confiança dos parâmetros do modelo
bi ± tn − p × (Erro Padrão de bi)
O uso de matrizes facilita sobremaneira o cálculo dos “erros padrão” dos parâmetros. E isso é feito pelo cálculo da “Matriz de Covariância” dos parâmetro como mostra a figura Y.5
E essa matriz pode ser calculada pela equação Y.3
Equação Y.3. Equação para o cálculo da matriz de covariância dos parâmetros do modelo
V(b) = (XtX)−1 σ2
O primeiro termo da equação já está disponível pois foi usado para o cálculo dos coeficientes do modelo e corresponde à variável X_t_dot_X.
Resta apenas estimar a variância das observações ( σ2 - erro experimental), e para isso temos três maneiras diferentes:
Através da Média Quadrática dos Resíduos da tabela ANOVA
Considerando os efeitos de interação de mais alta ordem (Ex: interações de três ou mais fatores) como flutuações (ruídos) embutidos nas respostas e utilizá-los para estimar o erro experimental nos valores dos modelos
Usando o desvio padrão de replicatas no “ponto central”.
Para a montagem da tabela ANOVA é necessário executar os experimentos em “replicatas” (duplicatas ou triplicatas) para o cálculo de resíduos (diferença entre os valores experimentais e os valores previstos pelo modelo).
Mas para planejamentos com muitos fatores e experimentos laboriosos, essa estratégia pode representar um aumento substancial no número de experimentos, podendo anular, de certa forma, uma das vantagens do planejamento fatorial que é otimizar o trabalho experimental.
Por outro lado para considerarmos que os efeitos de interação de mais alta ordem (Ex: interações de três ou mais fatores) sejam flutuações (ruídos) embutidos nas respostas precisamos “supor” que eles não são “estatísticamente significativos”.
Em alguns casos a diferença numérica entre os efeitos principais e efeitos secundários são suficientemente nítidas permitindo fazer essa suposição com alguma segurança. Mas podem surgir situações em que essa diferença não seja tão explícita, e nesses casos a análise fica sujeita a uma interpretação subjetiva.
A terceira alternativa é realizar experimentos no chamado “ponto central” do planejamento, no qual todos os fatores estão no nível “intermediário”, ou seja, após a codificação os fatores passam a assumir o nível “0”.
O ponto central pode ser considerado como a “condição inicial” do planejamento e pode ser usado para várias finalidades.
Por exemplo, uma única determinação da resposta no ponto central pode ser usada para avaliar a “curvatura” (termo quadrático) do modelo que relaciona a variável dependente (resposta) às variáveis independentes (fatores).
E a realização de ensaios em replicatas no ponto central do planejamento permite estimar a incerteza experimental (erro experimental ou erro puro) através da equação Y.4.
Onde:
yi = resposta do experimento i no ponto central
 = valor médio das respostas no ponto central (y_medio)
= valor médio das respostas no ponto central (y_medio)
N = número de replicatas no ponto central
Mas como definir um ponto central para uma variável “qualitativa” (ou categórica), como no caso do Catalisador que só pode assumir 2 estados (A ou B)?
Nesses casos, uma estratégia que pode ser adotada é fazer n replicatas com o nível alto (+1) da variável qualitativa e mais n replicatas com o nível baixo (-1) da variável qualitativa.
Nesse caso, vamos considerar que foram feitos mais 4 experimentos no ponto central para o estudo da variação do rendimento da reação em função da temperatura. Neste caso o novo planejamento com ponto central está indicado na tabela Y.5.
Tabela Y.5. Matriz de planejamento com “ponto central” para o estudo da variação do rendimento da reação em função da temperatura, com 2 replicatas na Temperatura de 50°C e Catalisador A, e mais 2 replicatas na Temperatura de 50°C, e o Catalisador B.
| Experimento (ou Ensaio) | Temperatura (°C) | Catalisador | Rendimento (%) |
|---|---|---|---|
| 1 | 40 | A | 59 |
| 2 | 40 | B | 54 |
| 3 | 60 | A | 90 |
| 4 | 60 | B | 68 |
| 5 | 50 | A | 67,5 |
| 6 | 50 | A | 69,4 |
| 7 | 50 | B | 64,35 |
| 8 | 50 | B | 64,14 |
Aplicando a equação Y.4 com os rendimentos das 4 replicatas no ponto central obtemos uma variância de 6,5.
A variância calculada a partir dos experimentos no Ponto Central pode agora ser usada para determinar a variância dos parâmetros do modelo estatístico usando a equação Y.3.
Mas é importante também lembrar que para o cálculo do intervalo de confiança através da equação Y.2 vamos precisar do valor de t de Student para n − p graus de liberdade, onde n = número de experimentos realizados e p = número de parâmetros.
E como foram feitos 4 experimentos e determinados 4 parâmetros (coeficientes) do modelo, n − p = “0”.
Neste caso as respostas obtidos dos experimentos no Ponto Central podem ser incluídas na Matriz de Planejamento para o cálculo dos parâmetros do modelo e consequente aumento do número de “graus de liberdade”.
Vamos importar as bibliotecas NumPy, Pandas e itertools, Statistics e scipy.stats:
>>> import numpy as np >>> import pandas as pd >>> import itertools >>> import statistics >>> from scipy.stats import t
Solicitar o número de fatores (Ex: n=2) e armazenar na variável n_factors:
>>> n_factors = int(input("Por favor, digite o número de fatores: "))
Por favor, digite o número de fatores: 2
>>>
Gerar todas as combinações dos fatores nos níveis alto e baixo e armazenar na variável exp_plan_coded_var, que corresponde à “matriz de planejamento com variáveis codificadas”:
>>> exp_plan_coded_var = np.array(list(itertools.product([-1,1], repeat = n_factors)))
>>> exp_plan_coded_var
array([[-1, -1],
[-1, 1],
[ 1, -1],
[ 1, 1]])
Dica
No ponto central os fatores são indicados pelo código “0” na matriz de planejamento com variáveis codificadas. E se todos os fatores forem quantitativos os experimentos no ponto central podem ser incluídos na variável que representa a matriz de planejamento (exp_plan_coded_var) com os comandos:
n_central_point = int(input("Por favor, digite o número de experimentos no Ponto Central: "))
Por favor, digite o número de experimentos no Ponto Central: 4
>>> exp_central_point = np.zeros((n_central_point, n_factors), dtype=int)
>>> exp_central_point
array([[0, 0],
[0, 0],
[0, 0],
[0, 0]])
>>> exp_plan_coded_var
array([[-1, -1],
[-1, 1],
[ 1, -1],
[ 1, 1]])
>>> exp_plan_coded_var = np.vstack([exp_plan_coded_var, exp_central_point])
>>> exp_plan_coded_var
array([[-1, -1],
[-1, 1],
[ 1, -1],
[ 1, 1],
[ 0, 0],
[ 0, 0],
[ 0, 0],
[ 0, 0]])
Mas neste caso o fator Catalisador é “qualitativa” (ou categórico) e portanto temos que fazer a inclusão “manual”.
>>> cp1 = np.array([0, -1])
>>> cp2 = np.array([0, 1])
>>> exp_plan_coded_var
>>> exp_plan_coded_var = np.vstack([exp_plan_coded_var, cp1])
>>> exp_plan_coded_var = np.vstack([exp_plan_coded_var, cp1])
>>> exp_plan_coded_var = np.vstack([exp_plan_coded_var, cp2])
>>> exp_plan_coded_var = np.vstack([exp_plan_coded_var, cp2])
>>> exp_plan_coded_var
array([[-1, -1],
[-1, 1],
[ 1, -1],
[ 1, 1],
[ 0, -1],
[ 0, -1],
[ 0, 1],
[ 0, 1]])
>>>
E implementar um loop for que solicita o nome de cada fator, com os respectivos limites superior (+1) e inferior (-1), e cria um identificador para cada fator (x1, x2, ... xn), que será a chave principal do dicionário dict_factors:
>>> dict_factors = {}
>>> for i in range(n_factors):
... code_factor = 'x' + str(i+1)
... name = input("Por favor, digite o nome do fator %d :" % (i+1))
... name_factor = name
... level_inf = input("Por favor, digite o nível INFERIOR do fator %d :" % (i+1))
... level_sup = input("Por favor, digite o nível SUPERIOR do fator %d :" % (i+1))
... dict_factors[code_factor] = {'name_factor' : name_factor, 'level_sup' : level_sup, 'level_inf' : level_inf, 'id_column' : i}
...
Por favor, digite o nome do fator 1 :Temperatura
Por favor, digite o nível INFERIOR do fator 1 :40
Por favor, digite o nível SUPERIOR do fator 1 :60
Por favor, digite o nome do fator 2 :Catalisador
Por favor, digite o nível INFERIOR do fator 2 :B
Por favor, digite o nível SUPERIOR do fator 2 :A
>>>
Cópia da matriz exp_plan_coded_var (Matriz de Planejamento com Variáveis Codificadas) para a matriz contrast_coef_table (Tabela de Coeficientes de Contraste). E ordenamento das “chaves” (keys) do dicionário dict_factors na variável lista sorted_factors.
>>> contrast_coef_table = np.copy(exp_plan_coded_var)
>>> sorted_factors = sorted(dict_factors, key=lambda x: (dict_factors[x]['id_column']))
>>> contrast_coef_table
array([[-1, -1],
[-1, 1],
[ 1, -1],
[ 1, 1],
[ 0, -1],
[ 0, -1],
[ 0, 1],
[ 0, 1]])
>>> sorted_factors
['x1', 'x2']
>>>
Sequência de 3 loops for aninhados para montar a lista com todas as possíveis interações entre os fatores e uma lista com todos os termos do modelo estatístico.
>>> list_all_interactions = []
>>> list_all_terms_of_statistical_model = []
>>> for f in sorted_factors:
... list_all_terms_of_statistical_model.append(f)
...
>>> for n in range(2, n_factors+1):
... list_interactions = list(itertools.combinations(sorted_factors, n))
... list_all_interactions.append(list_interactions)
... for c in range(len(list_interactions)):
... n_factors_in_combination = len(list_interactions[c])
... list_all_terms_of_statistical_model.append(list_interactions[c])
... temp_column = np.ones((exp_plan_coded_var.shape[0], 1))
... for f in range(len(list_interactions[c])):
... dict_factors_key = list_interactions[c][f]
... id_column_of_factor = dict_factors[dict_factors_key]['id_column']
... selected_column_coded_var = exp_plan_coded_var[:, id_column_of_factor].reshape(-1,1)
... temp_column = np.multiply(temp_column, selected_column_coded_var)
... contrast_coef_table = np.hstack([contrast_coef_table, temp_column])
...
>>> contrast_coef_table
array([[-1., -1., 1.],
[-1., 1., -1.],
[ 1., -1., -1.],
[ 1., 1., 1.],
[ 0., -1., -0.],
[ 0., -1., -0.],
[ 0., 1., 0.],
[ 0., 1., 0.]])
>>> contrast_coef_table.shape
(8, 3)
Complementar a “Tabela de Coeficientes de Contraste” adicionando uma coluna de “uns” à esquerda que permitirá calcular a “média das respostas”:
>>> column_ones = np.ones((exp_plan_coded_var.shape[0],1))
>>> contrast_coef_table = np.hstack([column_ones, contrast_coef_table])
>>> contrast_coef_table
array([[ 1., -1., -1., 1.],
[ 1., -1., 1., -1.],
[ 1., 1., -1., -1.],
[ 1., 1., 1., 1.],
[ 1., 0., -1., -0.],
[ 1., 0., -1., -0.],
[ 1., 0., 1., 0.],
[ 1., 0., 1., 0.]])
Os resultados de rendimento obtidos nos experimentos indicados na tabela Y.5 são organizados em um arquivo “csv” com a seguinte estrutura:
Rendimento 59 54 90 68 67,5 69,4 64,35 64,14
Em seguida usar o comando input e digitar o nome do arquivo, que foi chamado de Rend_Plan_Exp_Temp_Cat_Ponto_Central.csv.
Abrir o arquivo e armazenar como um dataframe na variável Y_df:
>>> Y_df = pd.read_csv(Y_csv_file, sep = ';', decimal=',') >>> Y_df Rendimento 0 59.00 1 54.00 2 90.00 3 68.00 4 67.50 5 69.40 6 64.35 7 64.14 >>>
E converter os rendimentos do formato “dataframe” para um “array”:
>>> Y = Y_df.values[:]
>>> Y
array([[59. ],
[54. ],
[90. ],
[68. ],
[67.5 ],
[69.4 ],
[64.35],
[64.14]])
Com as informações necessárias disponíveis executar as operações para o cálculo da matriz (B) com os coeficientes do modelo estatístico correspondente ao planejamento.
Matriz transposta de X (X_t), e o produto matricial de X_t por X:
>>> X
array([[ 1., -1., -1., 1.],
[ 1., -1., 1., -1.],
[ 1., 1., -1., -1.],
[ 1., 1., 1., 1.],
[ 1., 0., -1., -0.],
[ 1., 0., -1., -0.],
[ 1., 0., 1., 0.],
[ 1., 0., 1., 0.]])
>>> X_t = X.T
>>> X_t
array([[ 1., 1., 1., 1., 1., 1., 1., 1.],
[-1., -1., 1., 1., 0., 0., 0., 0.],
[-1., 1., -1., 1., -1., -1., 1., 1.],
[ 1., -1., -1., 1., -0., -0., 0., 0.]])
>>> X_t_dot_X = np.dot(X_t, X)
>>> X_t_dot_X
array([[8., 0., 0., 0.],
[0., 4., 0., 0.],
[0., 0., 8., 0.],
[0., 0., 0., 4.]])
Inversão da matriz X_t_dot_X:
>>> inv_X_t_dot_X = np.linalg.inv(X_t_dot_X)
>>> inv_X_t_dot_X
array([[0.125, 0. , 0. , 0. ],
[0. , 0.25 , 0. , 0. ],
[0. , 0. , 0.125, 0. ],
[0. , 0. , 0. , 0.25 ]])
>>>
Produto matricial de X_t por Y:
>>> X_t_dot_Y = np.dot(X_t, Y)
>>> X_t_dot_Y
array([[536.39],
[ 45. ],
[-35.41],
[-17. ]])
Cálculo da matriz de coeficientes do modelo (B):
>>> B = np.dot(inv_X_t_dot_X, X_t_dot_Y)
>>> B
array([[67.04875],
[11.25 ],
[-4.42625],
[-4.25 ]])
Com os coeficientes do modelo estatístico podemos “simular” os valores de rendimento com o comando:
>>> Y_sim = np.dot(X, B)
>>> Y_sim
array([[55.975 ],
[55.6225],
[86.975 ],
[69.6225],
[71.475 ],
[71.475 ],
[62.6225],
[62.6225]])
E comparar com os valores experimentais:
>>> Y
array([[59. ],
[54. ],
[90. ],
[68. ],
[67.5 ],
[69.4 ],
[64.35],
[64.14]])
Montar o modelo estatístico que será armazenado na variável statistical_model:
>>> statistical_model = str(B.item(0))
>>> statistical_model
'67.04875'
>>> for coef, factor in zip(B[1:], list_all_terms_of_statistical_model):
... if coef.item() > 0:
... statistical_model = statistical_model + ' +'
... statistical_model = statistical_model + str("%.4f" % coef.item()) + ' * '
... statistical_model = statistical_model + str(factor)
... statistical_model = statistical_model + ' '
...
>>> statistical_model
"67.04875 +11.2500 * x1 -4.4263 * x2 -4.2500 * ('x1', 'x2') "
Extraindo os rendimentos no ponto central e convertendo para o formato de “lista”:
>>> Y_central_point = Y[4:,]
>>> Y_central_point
array([[67.5 ],
[69.4 ],
[64.35],
[64.14]])
>>> Y_central_point = Y_central_point.flatten()
>>> Y_central_point
array([67.5 , 69.4 , 64.35, 64.14])
>>> Y_central_point = Y_central_point.tolist()
>>> Y_central_point
[67.5, 69.4, 64.35, 64.14]
Determinando o erro experimental:
>>> experimental_error = statistics.variance(Y_central_point) >>> experimental_error 6.503025000000019
Calculando a matriz de covariância dos parâmetros do modelo pela equação Y.3:
>>> matriz_covar = inv_X_t_dot_X * experimental_error
>>> matriz_covar
array([[0.81287813, 0. , 0. , 0. ],
[0. , 1.62575625, 0. , 0. ],
[0. , 0. , 0.81287813, 0. ],
[0. , 0. , 0. , 1.62575625]])
Extraindo a diagonal principal:
>>> V_B = np.diag(matriz_covar) >>> V_B array([0.81287813, 1.62575625, 0.81287813, 1.62575625])
Calculando o Erro Padrão dos coeficientes do modelo:
>>> standard_error_B = np.sqrt(V_B) >>> standard_error_B array([0.90159754, 1.27505147, 0.90159754, 1.27505147])
Obtendo o valor de t crítico:
>>> N = X.shape[0] >>> P = B.shape[0] >>> t_crit = t.ppf(1-0.025, N-P) >>> t_crit 2.7764451051977987
Calculando o intervalo de confiança e verificando a significância dos coeficientes do modelo:
>>> i = 0
>>> for par_b, erro_b in zip(B, standard_error_B):
... print("Parâmetro: %f e Erro: %f" % (par_b.item(), erro_b))
... intervalo = t_crit * erro_b
... print ("Intervalo: ", intervalo)
... b_max = par_b.item() + intervalo
... b_min = par_b.item() - intervalo
... print("Intervalo de confiança do parâmetro b%d (%f), limite superior (%f) e limite inferior (%f)" % (i, par_b.item(), b_max, b_min))
... print ("Isto significa que há 95%s de probabilidade de que o verdadeiro valor do parâmetro b%d esteja entre %f e %f" % ('%', i, b_min, b_max))
... if abs(intervalo) > abs(par_b.item()):
... print ("Como esses dois limites têm sinais contrários, e como nenhum valor num intervalo de confiança é mais provável do que outro, pode ser que o verdadeiro valor de b%d seja zero. Ou seja, o valor de b%d = %f não é estatisticamente significativo e portanto não existe evidência suficiente para manter o termo b%d no modelo." % (i, i, par_b.item(), i))
... print()
... i += 1
...
Parâmetro: 67.048750 e Erro: 0.901598
Intervalo: 2.5032360781247123
Intervalo de confiança do parâmetro b0 (67.048750), limite superior (69.551986) e limite inferior (64.545514)
Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b0 esteja entre 64.545514 e 69.551986
Parâmetro: 11.250000 e Erro: 1.275051
Intervalo: 3.5401104115056046
Intervalo de confiança do parâmetro b1 (11.250000), limite superior (14.790110) e limite inferior (7.709890)
Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b1 esteja entre 7.709890 e 14.790110
Parâmetro: -4.426250 e Erro: 0.901598
Intervalo: 2.5032360781247123
Intervalo de confiança do parâmetro b2 (-4.426250), limite superior (-1.923014) e limite inferior (-6.929486)
Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b2 esteja entre -6.929486 e -1.923014
Parâmetro: -4.250000 e Erro: 1.275051
Intervalo: 3.5401104115056046
Intervalo de confiança do parâmetro b3 (-4.250000), limite superior (-0.709890) e limite inferior (-7.790110)
Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b3 esteja entre -7.790110 e -0.709890
>>>
Os intervalos de confiança não incluem o 0 e portanto pode-se concluir que todos os coeficientes são significativos.
Mas pode-se verificar que o limite inferior da interação T×C ficou próximo de 0 e portanto podemos considerar como um efeito “de baixa significância”.
Nota
Os comandos usados nesta seção estão organizados em um único arquivo disponível no link: plan_exp_00.py.