Nota
Referências utilizadas nessa seção: Chemometrics - Data Driven Extraction for Science, 2018, Introduction to multivariate statistical analysis in chemometrics, 2009, Uma Introdução à Análise Exploratória de Dados Multivariados, 1998, Introduction to multivariate calibration in analytical chemistry, 2000 e Introduction to Multivariate Calibration - A Practical Approach, 2018
Nessa seção vamos mostrar a aplicação prática da técnica de PCR (Principal Components Regression - PCR ou Regressão sobre os Componentes Principais) na qual a Análise de Regressão Multivariada - MLR é associada à técnica de Análise de Componentes Principais - PCA no desenvolvimento de Modelos Empíricos (ou Estocásticos) a partir de dados experimentais multivariados “comprimidos” pela técnica de PCA.
Neste caso o objetivo é encontrar uma equação matemática que permita estabelecer a relação entre uma variável “dependente” (usualmente representada por y) com os “Componentes Principais” obtidos a partir das “variáveis originais”.
A análise de componentes principais (PCA) pode ser considerada como “a mãe de todos os métodos na análise de dados multivariados”. E é provavelmente a técnica quimiométrica multivariada mais difundida e, devido à importância das medições multivariadas em química, é considerada, por muitos, como a técnica que mais mudou a visão de análise de dados dos profissionais que atuam na área de Química.
A análise de componentes principais consiste em reescrever as variáveis originais em novas variáveis denominadas componentes principais, através de uma transformação de coordenadas. E essas “variáveis”, chamadas de Componentes Principais, são geradas através de uma transformação matemática especial realizada sobre as variáveis originais.
Cada componente principal é uma combinação linear de todas as variáveis originais. Por exemplo, a transformação de um sistema com dez variáveis, gera dez componentes principais. Cada uma destas componentes principais, por sua vez, será escrita como uma “combinação linear” das dez variáveis originais.
As componentes principais são “ortogonais” entre si, isso significa que as eventuais “correlações” que possam existir entre as variáveis originais são suprimidas nas componentes principais.
As componentes principais são “independentes” entre si e, portanto, trazem diferentes “informações estatísticas” sobre a variável dependente (resposta).
Outra importante característica é que as componentes principais são obtidos em ordem decrescente de máxima variância, ou seja, a componente principal 1 contém mais informação estatística que a componente principal 2, que por sua vez tem mais informação estatística que a componente principal 3 e assim por diante.
Isso permite a redução da dimensionalidade dos pontos representativos das amostras (compressão dos dados) pois, embora a informação estatística presente nas n-variáveis originais seja a mesma dos n-componentes principais, é comum obter em apenas 2 ou 3 das primeiras componentes principais mais que 90% desta informação.
Nota
Ou seja, as primeiras componentes principais são tão mais importantes que podemos até desprezar as demais.
A análise de componentes principais também pode ser usada para julgar a importância das próprias variáveis originais escolhidas, ou seja, as variáveis originais com maior peso (loadings) na combinação linear dos primeiros componentes principais são as mais importantes do ponto de vista estatístico.
A PCA visa transformar a matriz de dados X em uma matriz T com menor número de linhas mas o mesmo número de colunas de X como mostra a figura W.1.
Figura W.1. Diagrama da transformação da matriz de dados X na matriz de scores (T). (Fonte: Introduction to multivariate calibration in analytical chemistry, 2000)
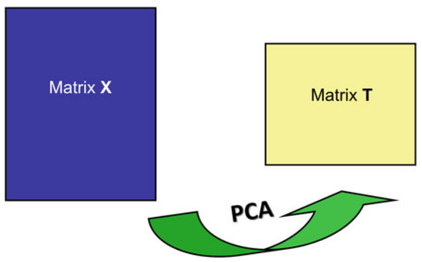
Essa transformação é feita pelo produto matricial da matriz de dados X com a matriz de “autovetores” (loadings - pesos) que vamos representar por “U”, segundo a equação W.1).
Onde:
T é a matriz de “scores” com o mesmo número de linhas da matriz de dados X. E onde cada coluna da matriz T representa um “Componente Principal”.
U é a matriz de “loadings”, pesos, com o número de linhas igual ao número de colunas da matriz de dados X
Cada coluna da matriz U corresponde a um “autovetor”.
Portanto, se a matriz de dados original (X) tiver dimensões 19 x 10 (ou I x J), só será possível calcular, no máximo, 10 Componentes Principais (PC).
E se o número de PCs for indicado por A:
As dimensões da matriz T (scores) será 19 x A
As dimensões da matriz U (loadings - pesos) será 10 x A
W.1. Exemplo de PCA com os dados de um Modelo Hidrológico
Vamos usar o conjunto de dados do Modelo Hidrológico para exemplificar inicialmente o uso da Análise de Componentes Principais usando Python para os cálculos.
Os dados originais podem não ter uma “distribuição” adequada dificultando a extração de informações e a interpretação dos mesmos. Por exemplo, quando duas ou mais variáveis (fatores) possuem valores numéricos (em diferentes unidades) ou diferentes variâncias.
Nesses casos é necessário fazer um pré-processamento dos dados originais usando as técnicas de centralização (centrar na média) e/ou autoescalar (padronização ou escalamento ou autoescalamento ou transformação z).
Dependendo da situação podem ser aplicadas apenas uma ou ambas as técnicas.
Os dados multivariados são organizados em uma matriz “X”, onde cada linha “i” representa uma amostra e cada coluna “j” representa uma propriedade (ou variável ou fator ou característica). E “xij” representa um elemento da linha “i” e coluna “j” da matriz “X” como mostra a figura W.2)
Figura W.2. Diagrama da matriz X, de dados multivariados, com “n” linhas (amostras, objetos) e “m” colunas (propriedades, variáveis, parâmetros, característica). (Fonte: Introduction to multivariate statistical analysis in chemometrics, 2009)
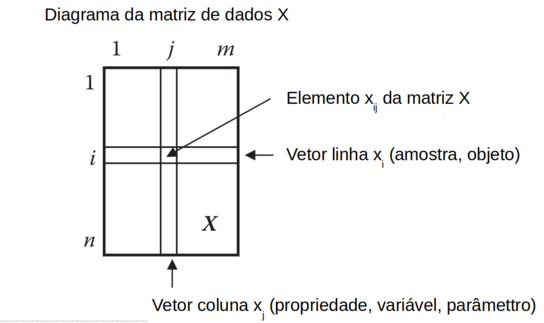
A centralização é feita calculando a média de cada variável e subtraindo-se cada variável do respectivo valor médio (Equação W.2).
Com a centralização as variáveis passam a ter média igual a “0”.
E o autoescalamento (ou padronização) significa centrar os dados na média e dividí-los pelo respectivo desvio padrão (Equação W.3).
Onde sj é o desvio padrão dos dados da coluna “j”.
Os dados escalados apresentam média zero e variância igual a “1” e tem como objetivo fazer com que todas as variáveis apresentem o mesmo “peso estatístico”.
O escalamento desloca o “centróide” dos dados para a origem e altera a escala dos eixos e consequentemente as distâncias relativas entre as amostras. Mas preserva as variâncias originais das variáveis como mostra a figura W.3)
Figura W.3. Representação gráfica dos efeitos da centralização na média e do escalamento dos dados de uma matriz X com 2 variáveis (x1 e x2). (Fonte: Introduction to multivariate statistical analysis in chemometrics, 2009)

Vamos abrir o arquivo de dados rainfall.csv (usado na seção Modelo Hidrológico) que deve estar no diretório local.
Mas antes carregar as bibliotecas NumPy, Pandas e Matplotlib.
import numpy as np import pandas as pd import matplotlib.pyplot as plt
E então abrir o arquivo rainfall.csv, que deve estar no diretório local.
data = pd.read_csv('rainfall.csv', sep=',')
Os dados são armazenados na variável data, do tipo “dataframe”, com a seguinte estrutura:
>>> data
Ano x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 y
0 1979 1948 4177 5496 2922 5713 3640 3203 2739 2167 2299 3255.2
1 1980 2261 3670 7797 3327 6934 4424 3692 3451 2866 2653 3682.7
2 1981 1989 4353 7392 2837 6275 4827 4476 4403 3568 3241 3921.9
3 1982 1999 3307 7061 3439 6641 4815 4256 4129 3447 3046 3909.3
4 1983 2086 4230 6564 2987 6675 3959 3900 3559 4078 3583 3768.9
5 1984 1717 2714 5919 3394 5605 3648 3085 2440 2631 2587 3106.4
6 1985 1383 2357 5053 2958 5144 3106 4052 3006 3049 2890 3069.4
7 1986 1470 3004 3951 2691 5116 3557 2775 1909 1952 1723 2940.2
8 1987 1350 2446 4280 2397 4722 3556 2818 2945 2931 2733 3015.3
9 1988 1602 4188 5910 3619 6869 5142 3190 3660 3964 3107 3953.2
10 1989 1417 3631 5145 3282 5226 3793 2663 3017 2579 3367 3172.4
11 1990 1662 4683 6384 6376 7313 4679 3037 3666 3142 2621 3791.0
12 1991 1955 4553 5679 6141 6068 3651 2601 2791 2148 2448 3344.8
13 1992 1974 3836 6021 5646 5876 4026 3037 3920 2583 2742 3650.3
14 1993 2094 4183 6733 6720 6044 6573 2465 3406 2410 2539 3878.7
15 1994 3149 6128 8151 9048 8384 7467 2888 3522 2496 2895 4606.2
16 1995 1471 2952 4151 4975 5149 4733 2603 3493 3396 3554 3498.8
17 1996 1691 3711 4200 4962 5359 3782 3185 3099 3381 2938 3241.0
18 1997 2373 4836 6704 6563 6197 5001 3902 3685 3636 3365 4013.5
>>>
Para realizar as operações matriciais com os comandos do Numpy, criamos a matriz de dados X extraindo as 10 primeiras colunas da variável data, e a matriz de escoamento Y com a última coluna da variável data.
X = data.values[:,1:11] Y = data.values[:,11]
A variável X é uma matriz bidimensional de 19 linhas por 10 colunas. Mas a matriz Y é um vetor unidimensional com 19 elementos:
>>> X.shape
(19, 10)
>>> Y
array([3255.2, 3682.7, 3921.9, 3909.3, 3768.9, 3106.4, 3069.4, 2940.2,
3015.3, 3953.2, 3172.4, 3791. , 3344.8, 3650.3, 3878.7, 4606.2,
3498.8, 3241. , 4013.5])
>>> Y.shape
(19,)
Por isso alteramos a dimensionalidade da variável Y com o comando reshape(-1,1):
>>> Y = Y.reshape(-1,1)
>>> Y
array([[3255.2],
[3682.7],
[3921.9],
[3909.3],
[3768.9],
[3106.4],
[3069.4],
[2940.2],
[3015.3],
[3953.2],
[3172.4],
[3791. ],
[3344.8],
[3650.3],
[3878.7],
[4606.2],
[3498.8],
[3241. ],
[4013.5]])
>>> Y.shape
(19, 1)
Vamos agora escalar os dados da matriz X, e centralizar os dados da matriz Y, usando basicamente os métodos mean e std da bublioteca numpy.
>>>X_scaled = (X - X.mean(axis = 0))/X.std(axis=0, ddof=1)
>>> X_scaled
array([[ 1.72188826e-01, 3.63397603e-01, -3.43849487e-01, -8.20025688e-01, -3.89046112e-01, -7.33961009e-01, -8.39355512e-02, -9.48167505e-01, -1.29125899e+00, -1.21196071e+00],
[ 8.92812996e-01, -1.83230928e-01, 1.49682098e+00, -6.00666109e-01, 9.45491926e-01, -1.55771999e-02, 7.19200604e-01, 2.39610068e-01, -1.66794322e-01, -4.46547779e-01],
[ 2.66583685e-01, 5.53154253e-01, 1.17284378e+00, -8.66064119e-01, 2.25213001e-01, 3.53694069e-01, 2.00684630e+00, 1.82776210e+00, 9.62496373e-01, 8.24816081e-01],
[ 2.89606821e-01, -5.74604018e-01, 9.08062414e-01, -5.40003706e-01, 6.25246516e-01, 3.42698399e-01, 1.64551715e+00, 1.37066793e+00, 7.67846552e-01, 4.03190311e-01],
[ 4.89908108e-01, 4.20540231e-01, 5.10490392e-01, -7.84819830e-01, 6.62408100e-01, -4.41659433e-01, 1.06082089e+00, 4.19778576e-01, 1.78292124e+00, 1.56428282e+00],
[-3.59645626e-01, -1.21395455e+00, -5.47329905e-03, -5.64376993e-01, -5.07088789e-01, -7.26630562e-01, -2.77739368e-01, -1.44696736e+00, -5.44833230e-01, -5.89251886e-01],
[-1.12861838e+00, -1.59885866e+00, -6.98224549e-01, -8.00527059e-01, -1.01095614e+00, -1.22326835e+00, 1.31046648e+00, -5.02750915e-01, 1.27593423e-01, 6.58896952e-02],
[-9.28317096e-01, -9.01287342e-01, -1.57976251e+00, -9.45141893e-01, -1.04155980e+00, -8.10014397e-01, -7.86884987e-01, -2.33279586e+00, -1.63712437e+00, -2.45737837e+00],
[-1.20459473e+00, -1.50290217e+00, -1.31658103e+00, -1.10438070e+00, -1.47219697e+00, -8.10930703e-01, -7.16261563e-01, -6.04512758e-01, -6.22303689e-02, -2.73573104e-01],
[-6.24411695e-01, 3.75257394e-01, -1.26727924e-02, -4.42510560e-01, 8.74447723e-01, 6.42330421e-01, -1.05286819e-01, 5.88269496e-01, 1.59953215e+00, 5.35083501e-01],
[-1.05033972e+00, -2.25279276e-01, -6.24629728e-01, -6.25039395e-01, -9.21331144e-01, -5.93766209e-01, -9.70834372e-01, -4.84400419e-01, -6.28484393e-01, 1.09725119e+00],
[-4.86272876e-01, 9.08947972e-01, 3.66500525e-01, 1.05075947e+00, 1.35973428e+00, 2.18080799e-01, -3.56574818e-01, 5.98278857e-01, 2.77200310e-01, -5.15737649e-01],
[ 1.88305021e-01, 7.68786810e-01, -1.97459789e-01, 9.23476749e-01, -1.03546208e-03, -7.23881644e-01, -1.07266350e+00, -8.61419705e-01, -1.32182384e+00, -8.89795383e-01],
[ 2.32048980e-01, -4.25590572e-03, 7.61209591e-02, 6.55370596e-01, -2.10889109e-01, -3.80266940e-01, -3.56574818e-01, 1.02200850e+00, -6.22049688e-01, -2.54113453e-01],
[ 5.08326618e-01, 3.69866580e-01, 6.45680878e-01, 1.23707970e+00, -2.72671680e-02, 1.95356413e+00, -1.29603061e+00, 1.64539856e-01, -9.00350671e-01, -6.93036691e-01],
[ 2.93726751e+00, 2.46689319e+00, 1.78000105e+00, 2.49799107e+00, 2.53032416e+00, 2.77274159e+00, -6.01293197e-01, 3.58054180e-01, -7.62004518e-01, 7.67006124e-02],
[-9.26014782e-01, -9.57351806e-01, -1.41977377e+00, 2.91937811e-01, -1.00549120e+00, 2.67561317e-01, -1.06937869e+00, 3.09675599e-01, 6.85804066e-01, 1.50157950e+00],
[-4.19505781e-01, -1.39026254e-01, -1.38057653e+00, 2.84896639e-01, -7.75963774e-01, -6.03845574e-01, -1.13498845e-01, -3.47605811e-01, 6.61673923e-01, 1.69674500e-01],
[ 1.15067212e+00, 1.07390688e+00, 6.22482511e-01, 1.15204402e+00, 1.39959957e-01, 5.13131292e-01, 1.06410570e+00, 6.29975169e-01, 1.07188635e+00, 1.09292683e+00]])
>>>X_scaled.mean(axis=0)
array([ 2.33731163e-16, 1.75298372e-16, 3.44753466e-16, 3.50596745e-17, 1.40238698e-16, -1.75298372e-17, 2.80477396e-16, -1.46081977e-16, -7.01193489e-17, -1.63611814e-16])
>>>X_scaled.std(axis=0, ddof=1)
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
Dica
Apenas para facilitar a visualização podemos formatar os números para apenas duas casas decimais com o comando round:
>>> X_scaled_formated = np.round(X_scaled, 2)
>>> X_scaled_formated
array([[ 0.17, 0.36, -0.34, -0.82, -0.39, -0.73, -0.08, -0.95, -1.29, -1.21],
[ 0.89, -0.18, 1.5 , -0.6 , 0.95, -0.02, 0.72, 0.24, -0.17, -0.45],
[ 0.27, 0.55, 1.17, -0.87, 0.23, 0.35, 2.01, 1.83, 0.96, 0.82],
[ 0.29, -0.57, 0.91, -0.54, 0.63, 0.34, 1.65, 1.37, 0.77, 0.4 ],
[ 0.49, 0.42, 0.51, -0.78, 0.66, -0.44, 1.06, 0.42, 1.78, 1.56],
[-0.36, -1.21, -0.01, -0.56, -0.51, -0.73, -0.28, -1.45, -0.54, -0.59],
[-1.13, -1.6 , -0.7 , -0.8 , -1.01, -1.22, 1.31, -0.5 , 0.13, 0.07],
[-0.93, -0.9 , -1.58, -0.95, -1.04, -0.81, -0.79, -2.33, -1.64, -2.46],
[-1.2 , -1.5 , -1.32, -1.1 , -1.47, -0.81, -0.72, -0.6 , -0.06, -0.27],
[-0.62, 0.38, -0.01, -0.44, 0.87, 0.64, -0.11, 0.59, 1.6 , 0.54],
[-1.05, -0.23, -0.62, -0.63, -0.92, -0.59, -0.97, -0.48, -0.63, 1.1 ],
[-0.49, 0.91, 0.37, 1.05, 1.36, 0.22, -0.36, 0.6 , 0.28, -0.52],
[ 0.19, 0.77, -0.2 , 0.92, -0. , -0.72, -1.07, -0.86, -1.32, -0.89],
[ 0.23, -0. , 0.08, 0.66, -0.21, -0.38, -0.36, 1.02, -0.62, -0.25],
[ 0.51, 0.37, 0.65, 1.24, -0.03, 1.95, -1.3 , 0.16, -0.9 , -0.69],
[ 2.94, 2.47, 1.78, 2.5 , 2.53, 2.77, -0.6 , 0.36, -0.76, 0.08],
[-0.93, -0.96, -1.42, 0.29, -1.01, 0.27, -1.07, 0.31, 0.69, 1.5 ],
[-0.42, -0.14, -1.38, 0.28, -0.78, -0.6 , -0.11, -0.35, 0.66, 0.17],
[ 1.15, 1.07, 0.62, 1.15, 0.14, 0.51, 1.06, 0.63, 1.07, 1.09]])
O parâmetro “axis=0” define que as médias e desvios-padrões devem ser calculados para cada coluna da matriz. E o parâmetro “ddof = 1” define que o desvio-padrão deve ser dividido por “N - 1”.
Comparando a média e desvio-padrão de cada coluna (variável) da matriz original (X):
>>> X.mean(axis=0)
array([1873.21052632, 3839.94736842, 5925.84210526, 4436. , 6068.94736842, 4441. , 3254.10526316, 3307.36842105, 2969.68421053, 2859.52631579])
>>> X.std(axis=0, ddof=1)
array([ 434.34568657, 927.50372708, 1250.08796416, 1846.28362453, 914.92334067, 1091.33862756, 608.86313868, 599.43883114, 621.62913673,
462.49544964])
Centralizando a matriz Y:
Y_centered = Y - Y.mean()
>>> Y_centered
array([[-314.23157895],
[ 113.26842105],
[ 352.46842105],
[ 339.86842105],
[ 199.46842105],
[-463.03157895],
[-500.03157895],
[-629.23157895],
[-554.13157895],
[ 383.76842105],
[-397.03157895],
[ 221.56842105],
[-224.63157895],
[ 80.86842105],
[ 309.26842105],
[1036.76842105],
[ -70.63157895],
[-328.43157895],
[ 444.06842105]])
A matriz de covariância é determinada com o comando np.cov, no entanto este comando precisa receber um array onde as linhas representam as variáveis, e as colunas representam as amostras. Por isso é necessário fazer a transposição da matriz X_scaled_t. (Fonte: X ao Quadrado)
>>> X_scaled_t = X_scaled.T
>>> X_scaled_cov = np.cov(X_scaled_t)
>>> X_scaled_cov
array([[ 1. , 0.79404489, 0.80990796, 0.63970323, 0.77521414, 0.71293954, 0.17691772, 0.37593752, -0.03410999, 0.08058727],
[ 0.79404489, 1. , 0.64635934, 0.72026928, 0.79650014, 0.68308169, -0.01513445, 0.39791947, 0.03326402, 0.12261396],
[ 0.80990796, 0.64635934, 1. , 0.37713523, 0.84059123, 0.63676163, 0.43663616, 0.61475783, 0.16903324, 0.1865701 ],
[ 0.63970323, 0.72026928, 0.37713523, 1. , 0.54535834, 0.7086409 , -0.35274604, 0.24628053, -0.15071195, 0.03522937],
[ 0.77521414, 0.79650014, 0.84059123, 0.54535834, 1. , 0.701949 , 0.21145731, 0.51174676, 0.20540401, 0.12513717],
[ 0.71293954, 0.68308169, 0.63676163, 0.7086409 , 0.701949 , 1. , -0.10305249, 0.47946345, 0.0833055 , 0.17971098],
[ 0.17691772, -0.01513445, 0.43663616, -0.35274604, 0.21145731, -0.10305249, 1. , 0.51872746, 0.59255388, 0.36865464],
[ 0.37593752, 0.39791947, 0.61475783, 0.24628053, 0.51174676, 0.47946345, 0.51872746, 1. , 0.63756523, 0.63699489],
[-0.03410999, 0.03326402, 0.16903324, -0.15071195, 0.20540401, 0.0833055 , 0.59255388, 0.63756523, 1. , 0.78544619],
[ 0.08058727, 0.12261396, 0.1865701 , 0.03522937, 0.12513717, 0.17971098, 0.36865464, 0.63699489, 0.78544619, 1. ]])
A matriz de covariância indica o grau de “correlação entre as variáveis”.
A figura W.4 mostra as matrizes de covariância para três diferentes conjuntos de dados com duas variáveis (x1 e x2).
Figura W.4. Matrizes de covariância para três diferentes distribuições de dados bidimensionais. (Fonte: Introduction to multivariate statistical analysis in chemometrics, 2009)
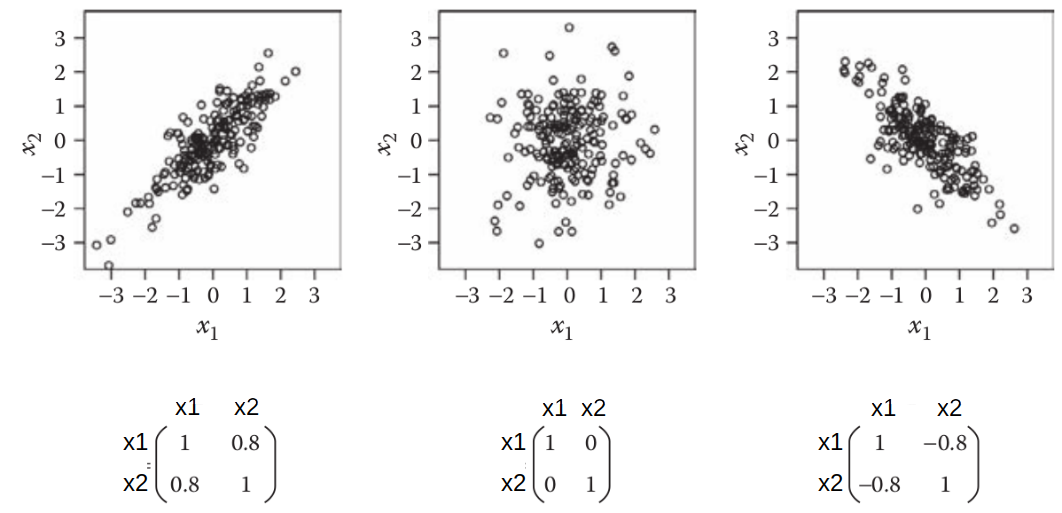
A próxima etapa é calcular os “autovetores” e “autovalores” da matriz de covariância usando o comando np.linalg.eig:
>>> eigen_values, eigen_vectors = np.linalg.eig(X_scaled_cov)
>>> eigen_values
array([4.94476901, 2.63104132, 1.04707047, 0.36402519, 0.04226097, 0.06291811, 0.3069196 , 0.25645457, 0.20463143, 0.13990933])
>>> eigen_vectors
array([[ 0.38978763, 0.1652208 , 0.21072082, -0.19078455, -0.07918716, 0.64354163, -0.45066908, -0.30387108, -0.14927571, -0.04272884],
[ 0.3806454 , 0.18765072, -0.05328529, -0.54336361, 0.15666345, -0.18937047, 0.1272609 , 0.21447465, 0.26478207, -0.57367594],
[ 0.39306036, -0.02940564, 0.38219638, 0.23534225, 0.60006525, -0.22727222, -0.07436552, -0.12807793, 0.3283922 , 0.31886083],
[ 0.29787865, 0.32096244, -0.39009458, -0.11084286, 0.08876735, -0.20996465, -0.24606337, 0.40030428, -0.425083 , 0.43628024],
[ 0.40412001, 0.06517945, 0.17945998, -0.12080663, -0.5217421 , 0.01335586, 0.58928364, -0.05631499, 0.09260475, 0.39273797],
[ 0.37070265, 0.16101943, -0.22862469, 0.54608635, -0.08664306, -0.2412643 , 0.11565508, -0.39407656, -0.30058576, -0.40178728],
[ 0.12185754, -0.46239873, 0.52101492, -0.11695236, -0.22854077, -0.39282174, -0.23664377, 0.14770144, -0.42828739, -0.13571246],
[ 0.31669491, -0.33762572, -0.12164964, 0.4435065 , -0.13475719, 0.3329343 , -0.06946022, 0.60350442, 0.2411245 , -0.1342702 ],
[ 0.13557434, -0.52896578, -0.23733692, -0.20135297, 0.44277958, 0.27474898, 0.41206563, -0.11032524, -0.38790353, 0.03103737],
[ 0.16027409, -0.44251959, -0.47691763, -0.19225426, -0.234653 , -0.23500463, -0.351241 , -0.3582497 , 0.35791414, 0.15482791]])
>>>
O comando np.linalg.eig retorna dois arrays: os autovalores eigen_values e os “respectivos” autovetores eigen_vectors.
Os maiores autovalores indicam os componentes principais (PCs) que mais contribuem para a “variância” dos dados. Mas eles não estão ordenados e, por isso, vamos primeiro ordenar em ordem decrescente para facilitar a seleção dos PCs mais importantes:
>>> idx = eigen_values.argsort()[::-1]
>>> eigen_values = eigen_values[idx]
>>> eigen_vectors = eigen_vectors[:,idx]
>>> eigen_values
array([4.94476901, 2.63104132, 1.04707047, 0.36402519, 0.3069196 , 0.25645457, 0.20463143, 0.13990933, 0.06291811, 0.04226097])
>>> eigen_vectors
array([[ 0.38978763, 0.1652208 , 0.21072082, -0.19078455, -0.45066908, -0.30387108, -0.14927571, -0.04272884, 0.64354163, -0.07918716],
[ 0.3806454 , 0.18765072, -0.05328529, -0.54336361, 0.1272609 , 0.21447465, 0.26478207, -0.57367594, -0.18937047, 0.15666345],
[ 0.39306036, -0.02940564, 0.38219638, 0.23534225, -0.07436552, -0.12807793, 0.3283922 , 0.31886083, -0.22727222, 0.60006525],
[ 0.29787865, 0.32096244, -0.39009458, -0.11084286, -0.24606337, 0.40030428, -0.425083 , 0.43628024, -0.20996465, 0.08876735],
[ 0.40412001, 0.06517945, 0.17945998, -0.12080663, 0.58928364, -0.05631499, 0.09260475, 0.39273797, 0.01335586, -0.5217421 ],
[ 0.37070265, 0.16101943, -0.22862469, 0.54608635, 0.11565508, -0.39407656, -0.30058576, -0.40178728, -0.2412643 , -0.08664306],
[ 0.12185754, -0.46239873, 0.52101492, -0.11695236, -0.23664377, 0.14770144, -0.42828739, -0.13571246, -0.39282174, -0.22854077],
[ 0.31669491, -0.33762572, -0.12164964, 0.4435065 , -0.06946022, 0.60350442, 0.2411245 , -0.1342702 , 0.3329343 , -0.13475719],
[ 0.13557434, -0.52896578, -0.23733692, -0.20135297, 0.41206563, -0.11032524, -0.38790353, 0.03103737, 0.27474898, 0.44277958],
[ 0.16027409, -0.44251959, -0.47691763, -0.19225426, -0.351241 , -0.3582497 , 0.35791414, 0.15482791, -0.23500463, -0.234653 ]])
>>> eigen_vectors.shape
(10, 10)
A matriz de “autovetores”, armazenada na variável eigen_vectors, corresponde à matriz de “Loadings” indicada na equação W.1 pela letra “U”, na qual o número de linhas é igual ao número de colunas da matriz de dados X.
Para gerar a matriz de “Scores” (T) vamos fazer a multiplicação matricial da matriz X escalonada (variável X_scaled) pela matriz de “Loadings” (U) (variável eigen_vectors) com o comando np.dot, como indicado na figura W.5.
Figura W.5. Cálculo da matriz de Scores (T) pelo produto matricial da matriz X escalonada pela matriz de Loadings (U)
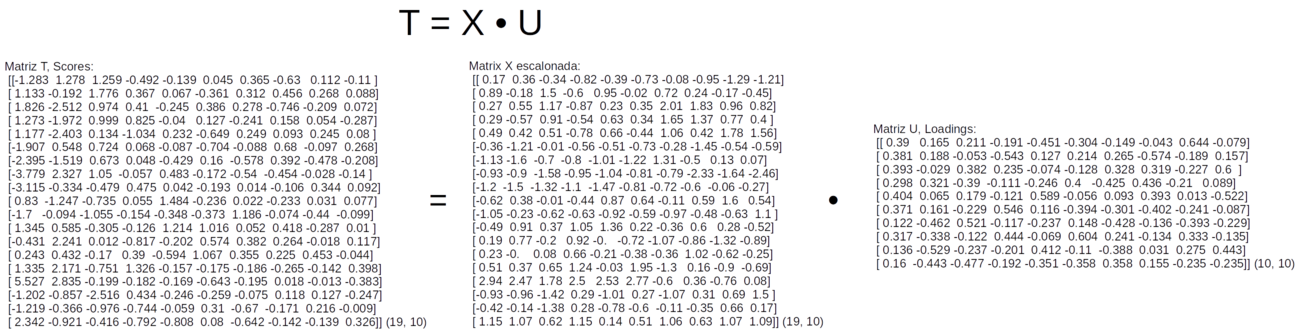
>>> T = np.dot(X_scaled, eigen_vectors)
>>> T
array([[-1.28309714, 1.27830047, 1.2594544 , -0.49184161, -0.13882027, 0.04456441, 0.36519792, -0.63014891, 0.1115388 , -0.10965111],
[ 1.13333476, -0.1921813 , 1.77565198, 0.36693434, 0.06744803, -0.3606542 , 0.3119507 , 0.45568254, 0.26795075, 0.08778733],
[ 1.8256902 , -2.51217403, 0.97380184, 0.41007612, -0.24519973, 0.38645935, 0.27758199, -0.74644501, -0.20943004, 0.07198327],
[ 1.27326984, -1.97230647, 0.99928305, 0.82546619, -0.04003459, 0.12712391, -0.24053406, 0.15798074, 0.05402214, -0.28729862],
[ 1.17652047, -2.40257204, 0.13438727, -1.03367649, 0.23219625, -0.64856091, 0.24873361, 0.09299442, 0.24509345, 0.07977901],
[-1.90722647, 0.54765669, 0.72374353, 0.06769209, -0.08729155, -0.70445884, -0.08768726, 0.68044435, -0.09713769, 0.2679342 ],
[-2.39511004, -1.51863557, 0.67326327, 0.04802125, -0.42891051, 0.16046961, -0.57819007, 0.39183307, -0.47772903, -0.20841667],
[-3.77906522, 2.32716534, 1.04991791, -0.05719857, 0.48303071, -0.17246854, -0.54002752, -0.45423269, -0.02759952, -0.13999633],
[-3.11464609, -0.33405051, -0.47933466, 0.47480795, 0.04187447, -0.19302665, 0.01362215, -0.10625641, 0.34378111, 0.09203759],
[ 0.83023933, -1.24679452, -0.73495656, 0.05469464, 1.48379631, -0.23635384, 0.02240463, -0.23255378, 0.03053853, 0.07692986],
[-1.70035914, -0.09436787, -1.05485152, -0.15356556, -0.34764879, -0.37296304, 1.18637675, -0.07384574, -0.43957273, -0.09887999],
[ 1.34478072, 0.58492142, -0.30494924, -0.12612551, 1.21370214, 1.01645747, 0.05218307, 0.41783535, -0.28681804, 0.01040458],
[-0.43059467, 2.24074373, 0.01230888, -0.8170393 , -0.20237914, 0.57424478, 0.38151434, 0.26373738, -0.01828512, 0.11702125],
[ 0.24293218, 0.43199222, -0.169628 , 0.3902063 , -0.59397365, 1.06668687, 0.35491022, 0.22520154, 0.45330486, -0.0442453 ],
[ 1.33542838, 2.17091288, -0.75098062, 1.32606627, -0.15687448, -0.17545968, -0.18556066, -0.26538531, -0.14170391, 0.39790738],
[ 5.52719211, 2.83530335, -0.19904172, -0.18249598, -0.16858564, -0.64278882, -0.19481687, 0.01814727, -0.01308174, -0.38290892],
[-1.20220629, -0.85696934, -2.51598068, 0.43358481, -0.24560323, -0.25870845, -0.07505439, 0.11835617, 0.12748409, -0.24729564],
[-1.21866803, -0.36641413, -0.97578786, -0.74366211, -0.05911022, 0.30985381, -0.67015837, -0.17148568, 0.21640409, -0.00859278],
[ 2.34158512, -0.92053032, -0.41630128, -0.79194482, -0.80761611, 0.07958276, -0.64244618, -0.1418593 , -0.13876 , 0.32550087]])
>>> T.shape
(19, 10)
Os valores experimentais (pluviométricos) da matriz X são chamados de valores “Reais”, e os valores da matriz T são chamodos valores “Latentes”. E são assim chamados porque não podem ser visualizados diretamente a partir dos valores experimentais mas somente após as operações matemáticas que revelam a sua presença. (Fonte: Introduction to Multivariate Calibration - A Practical Approach, 2018).
Agora algumas questões importantes:
- W.1.3.1. Mas afinal, o que a matriz T tem de especial?
- W.1.3.2. E pra que serve a matriz T?
- W.1.3.3. E como construir o modelo de regressão PCR?
W.1.3.1. | Mas afinal, o que a matriz T tem de especial? |
Cada “coluna” da matriz T corresponde a uma “componente principal”, e como são “ortogonais” entre si, significa que são também “independentes” entre si. Além disso, cada componente principal possui um “tipo de informação” a respeito da variável dependente (Y) mas com diferentes níveis de “conteúdo informacional” sobre a variável dependente (Y). | |
W.1.3.2. | E pra que serve a matriz T? |
Ela serve, entre outras coisas, para construir um Modelo de Regressão Multivariado baseado nas componentes principais como variáveis independentes e não mais nas variáveis originais. | |
W.1.3.3. | E como construir o modelo de regressão PCR? |
Vamos usar as mesmas equações da seção Modelos Empíricos com Regressão Linear Multivariada para construir um modelo que relacione a variável dependente Y com os Componentes Principais da matriz T. |
Agora as variáveis independentes serão os Componentes Principais que correspondem às colunas da matriz T. E a variável dependente será a matriz coluna Y que corresponde ao escoamento anual no ponto de saída da bacia.
Mas é importante lembrar que as Componentes Principais não correspondem às grandeza física (volume de chuvas) como nas variáveis originais da planilha X.
Cada Componente Principal é uma “entidade matemática abstrata” obtida pela “combinação linear das variáveis originais”.
Para o cálculo das estimativas dos parâmetros (β1, β2 ... β10) do modelo de Regressão por Componentes Principais (PCR), vamos utilizar novamente a Equação matricial geral para o ajuste de modelos pela técnica dos “mínimos quadrados”, mas agora usando a matriz T ao invés da matriz X:
B = (TtT)-1 TtY
A matriz transposta de T (T_t) é obtida com o método T:
>>> T_t = T.T
Dica
Exibindo apenas a versão formatada:
>>> T_t_formated = np.round(T_t, 2)
>>> T_t_formated
array([[-1.28, 1.13, 1.83, 1.27, 1.18, -1.91, -2.4 , -3.78, -3.11, 0.83, -1.7 , 1.34, -0.43, 0.24, 1.34, 5.53, -1.2 , -1.22, 2.34],
[ 1.28, -0.19, -2.51, -1.97, -2.4 , 0.55, -1.52, 2.33, -0.33, -1.25, -0.09, 0.58, 2.24, 0.43, 2.17, 2.84, -0.86, -0.37, -0.92],
[ 1.26, 1.78, 0.97, 1. , 0.13, 0.72, 0.67, 1.05, -0.48, -0.73, -1.05, -0.3 , 0.01, -0.17, -0.75, -0.2 , -2.52, -0.98, -0.42],
[-0.49, 0.37, 0.41, 0.83, -1.03, 0.07, 0.05, -0.06, 0.47, 0.05, -0.15, -0.13, -0.82, 0.39, 1.33, -0.18, 0.43, -0.74, -0.79],
[-0.14, 0.07, -0.25, -0.04, 0.23, -0.09, -0.43, 0.48, 0.04, 1.48, -0.35, 1.21, -0.2 , -0.59, -0.16, -0.17, -0.25, -0.06, -0.81],
[ 0.04, -0.36, 0.39, 0.13, -0.65, -0.7 , 0.16, -0.17, -0.19, -0.24, -0.37, 1.02, 0.57, 1.07, -0.18, -0.64, -0.26, 0.31, 0.08],
[ 0.37, 0.31, 0.28, -0.24, 0.25, -0.09, -0.58, -0.54, 0.01, 0.02, 1.19, 0.05, 0.38, 0.35, -0.19, -0.19, -0.08, -0.67, -0.64],
[-0.63, 0.46, -0.75, 0.16, 0.09, 0.68, 0.39, -0.45, -0.11, -0.23, -0.07, 0.42, 0.26, 0.23, -0.27, 0.02, 0.12, -0.17, -0.14],
[ 0.11, 0.27, -0.21, 0.05, 0.25, -0.1 , -0.48, -0.03, 0.34, 0.03, -0.44, -0.29, -0.02, 0.45, -0.14, -0.01, 0.13, 0.22, -0.14],
[-0.11, 0.09, 0.07, -0.29, 0.08, 0.27, -0.21, -0.14, 0.09, 0.08, -0.1 , 0.01, 0.12, -0.04, 0.4 , -0.38, -0.25, -0.01, 0.33]])
O produto matricial de T_t e T é obtido com o método dot(T_t,T) e armazenado na variável T_t_dot_T:
>>> T_t_dot_T = np.dot(T_t, T)
...
#Exibindo versão formatada com 2 casas decimais
...
array([[89.01, -0. , -0. , -0. , -0. , -0. , -0. , 0. , 0. , -0. ],
[-0. , 47.36, -0. , 0. , 0. , -0. , 0. , 0. , -0. , 0. ],
[-0. , -0. , 18.85, 0. , 0. , 0. , 0. , -0. , -0. , -0. ],
[-0. , 0. , 0. , 6.55, 0. , -0. , 0. , 0. , -0. , -0. ],
[-0. , 0. , 0. , 0. , 5.52, -0. , -0. , -0. , 0. , -0. ],
[-0. , -0. , 0. , -0. , -0. , 4.62, -0. , -0. , 0. , 0. ],
[-0. , 0. , 0. , 0. , -0. , -0. , 3.68, -0. , -0. , -0. ],
[ 0. , 0. , -0. , 0. , -0. , -0. , -0. , 2.52, -0. , 0. ],
[ 0. , -0. , -0. , -0. , 0. , 0. , -0. , -0. , 1.13, -0. ],
[-0. , 0. , -0. , -0. , -0. , 0. , -0. , 0. , -0. , 0.76]])
A matriz inversa de T_t_dot_T é calculada com o método linalg.inv(T_t_dot_T) e o resultado armazenado na variável inv_T_t_dot_T:
>>> inv_T_t_dot_T = np.linalg.inv(T_t_dot_T)
>>> inv_T_t_dot_T_formated = np.round(inv_T_t_dot_T, 2)
...
#Exibindo versão formatada com 2 casas decimais
...
array([[ 0.01, 0. , 0. , 0. , 0. , 0. , 0. , -0. , -0. , 0. ],
[ 0. , 0.02, 0. , -0. , -0. , 0. , -0. , -0. , 0. , -0. ],
[ 0. , 0. , 0.05, -0. , -0. , -0. , -0. , 0. , 0. , 0. ],
[ 0. , -0. , -0. , 0.15, -0. , 0. , -0. , -0. , 0. , 0. ],
[ 0. , -0. , -0. , -0. , 0.18, 0. , 0. , 0. , -0. , 0. ],
[ 0. , 0. , -0. , 0. , 0. , 0.22, 0. , 0. , -0. , -0. ],
[ 0. , -0. , -0. , -0. , 0. , 0. , 0.27, 0. , 0. , 0. ],
[-0. , -0. , 0. , -0. , 0. , 0. , 0. , 0.4 , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. , -0. , 0. , 0. , 0.88, 0. ],
[ 0. , -0. , 0. , 0. , 0. , -0. , 0. , -0. , 0. , 1.31]])
O segundo termo da equação é obtido pelo produto matricial das matrizes T_t e Y (centralizado):
>>> T_t_Y = np.dot(T_t,Y_centered)
>>> T_t_Y
array([[17103.50781303],
[ -628.68907763],
[ -624.3530756 ],
[ 484.4937618 ],
[ 353.92143734],
[ -72.35421949],
[ -178.87349552],
[ -194.20262911],
[ 63.83171093],
[ -62.58869785]])
>>>
E a matriz B com as estimativas dos parâmetros β1, β2 ... β10 da equação de regressão para os componentes principais pode então ser determinada com o produto matricial:
>>> B = np.dot(inv_T_t_dot_T, T_t_Y)
>>> B
array([[192.16163121],
[-13.27503704],
[-33.12697951],
[ 73.9408175 ],
[ 64.06336407],
[-15.67403896],
[-48.56251177],
[-77.11447854],
[ 56.36224805],
[-82.27803412]])
>>>
Cada elemento da matriz B é um dos coeficientes do modelo de regressão e portanto o modelo empírico “multivariado” que permite calcular o escoamento anual total da bacia (em mm) a partir dos “Componentes Principais” (calculados a partir dos registros de chuva anual dos 10 pluviômetros) pode ser agora expresso pela equação W.4.
Equação W.4. Modelo multivariado que descreve o volume de escoamento anual da bacia hidrográfica em função dos Componentes Principais calculados a partir dos registros de precipitação de 10 pluviômetros (x1, x2, x3, ... x10) instalados na bacia de drenagem.
yi = 192∗PC1i − 13,275∗PC2i − 33,127∗PC3i + 73,941∗PC4i + 64,063∗PC5i − 15,674∗PC6i − 48,562∗PC7i − 77,114∗PC8i + 56,362∗PC9i − 82,278∗PC10i
Os valores de escoamento da bacia “estimados” pelo modelo baseado em PC são obtidos pelo produto:
>>>Y_est_10_pc = np.dot(T, B) >>>Y_est_10_pc [[-305.04528302] [ 156.20847035] [ 386.82841006] [ 320.41268311] [ 190.13405068] [-463.02041221] [-500.74882337] [-691.23054914] [-518.0502308 ] [ 315.4808683 ] [-386.88599739] [ 261.47140057] [-244.79999813] [ 15.23579149] [ 332.17809857] [1055.67923422] [ -93.86418527] [-201.94999564] [ 371.96646761]]
Agora vamos demostrar uma das principais vantagens do modelo de regressão linear multivariado baseado em componentes principais (PCR).
Como já foi dito, os componente principais são “ortogonais” entre si, o que significa que são “independentes” entre si.
Para visualizar essa propriedade vamos colocar em um gráfico os valores de escoamento observados experimentalmente e os valores simulados usando o modelo de regressão liear a partir dos registros de precipitação de 10 pluviômetros (MLR) e o modelo de regressão linear a partir dos componentes principais (PCR).
Mas vamos verificar o que acontece com a capacidade de previsão dos modelos se retirarmos gradualmente os termos do modelo, como mostra a figura W.6.
Figura W.6. À esquerda o gráfico de correlação entre os valores observados experimentalmente e os valores obtidos em 3 simulações obtidas a partir do modelo de regressão (MLR) completo (1-10), com remoção de duas variáveis (1-8) e com remoção de 4 variáveis (1-6). E à direita o gráfico de correlação entre os valores observados experimentalmente e os valores obtidos em 3 simulações (PCR) obtidas a partir do modelo completo (1-10), com remoção de quatro variáveis (1-6) e com remoção de 8 variáveis (1-2).
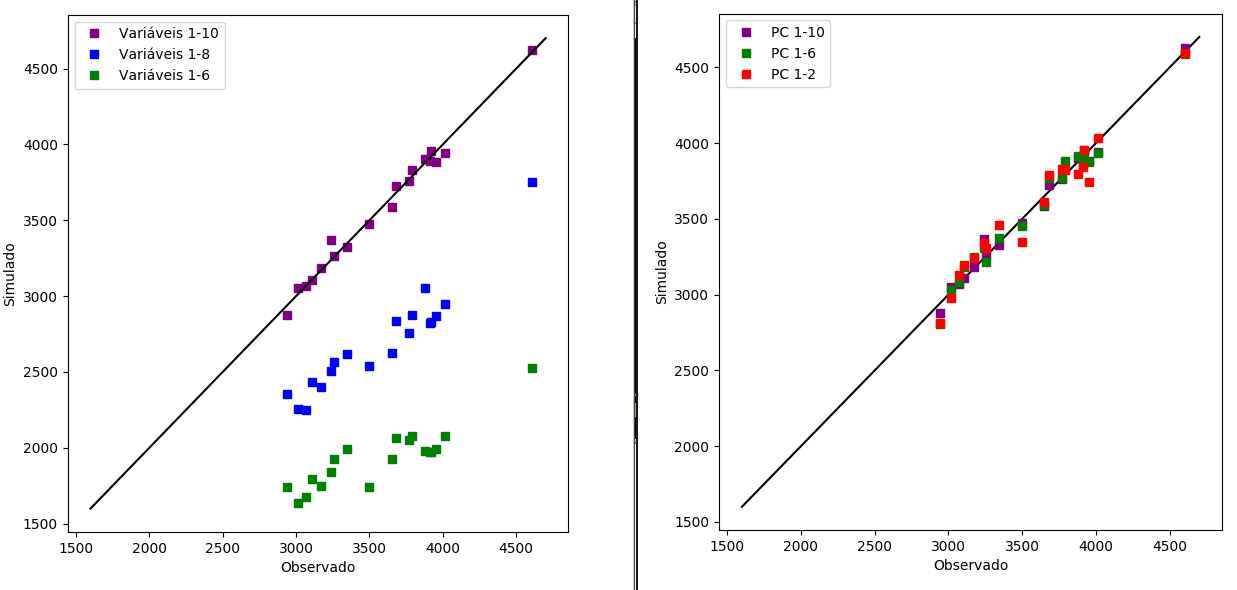
No gráfico à esquerda pode-se observar como a capacidade de previsão do modelo fica comprometida se retirarmos 2 ou mais variáveis. Mas o gráfico à direita mostra que com apenas as 2 primeiras componentes principais o modelo PCR consegue fazer previsões comparáveis ao modelo completo (com todos os 10 PCs).
Principal Component Analysis Tutorial Part 1 | Python Machine Learning Tutorial Part 3
How to Calculate Principal Component Analysis (PCA) from Scratch in Python
Comentários importantes sobre as vantagens do SVD e os riscos de centralizar na média
In many problems our features are positive values such as counts of words or pixel intensities. Typically a higher count or a higher pixel intensity means that a feature is more useful for classification/regression. If you subtract the means then you are forcing features with original value of zero to have a negative value which is high in magnitude. This entails that you make the features values that are non-important to the problem of classification (previously zero valued) as influential as the most important features values (the ones that have high counts or pixel intensities).
The same reasoning holds for PCA. If your features are least sensitive (informative) towards the mean of the distribution, then it makes sense to subtract the mean. If the features are most sensitive towards the high values, then subtracting the mean does not make sense.
How to reverse PCA and reconstruct original variables from several principal components?
Making sense of principal component analysis, eigenvectors & eigenvalues